Buying Price
The get_buy_price function at 0x0052E430 takes a ware, town, and buy amount and returns the transaction price.
Formula
The price formula operates on 5 intervals, and the 4 price thresholds specify the bounds.
| Interval | Bounds |
|---|---|
| 0 | [0; \(t_0\)] |
| 1 | [\(t_0\); \(t_1\)] |
| 2 | [\(t_1\); \(t_2\)] |
| 3 | [\(t_2\); \(t_3\)] |
| 4 | [\(t_3\); \(\infty\)] |
Within every interval \(i\) the price \(p_i\) is defined as: \[ \begin{aligned} p_{i} &= p_{base} * w_{i} * f_{i} \end{aligned} \]
where \(w_i\) is the amount being bought from \(i\) and \(f\) is defined as: \[ \begin{aligned} f_4 &= 0.6\\ f_{i} &= m_i - v_i \underbrace{\frac{w_{relative\_stock} + w_{relative\_remain}}{2 * \text{interval_width}}}_{\in [0; 1]} \end{aligned} \]
where \(w_{relative\_stock}\) and \(w_{relative\_remain}\) are the stock's and remainder's offsets in the interval and \(m_i\) and \(v_i\) are defined as:
| Interval | \(m_i\) | \(v_i\) |
|---|---|---|
| 0 | 4 | 2.5 |
| 1 | 1.5 | 0.5 |
| 2 | 1.0 | 0.2 |
| 3 | 0.8 | 0.2 |
Example
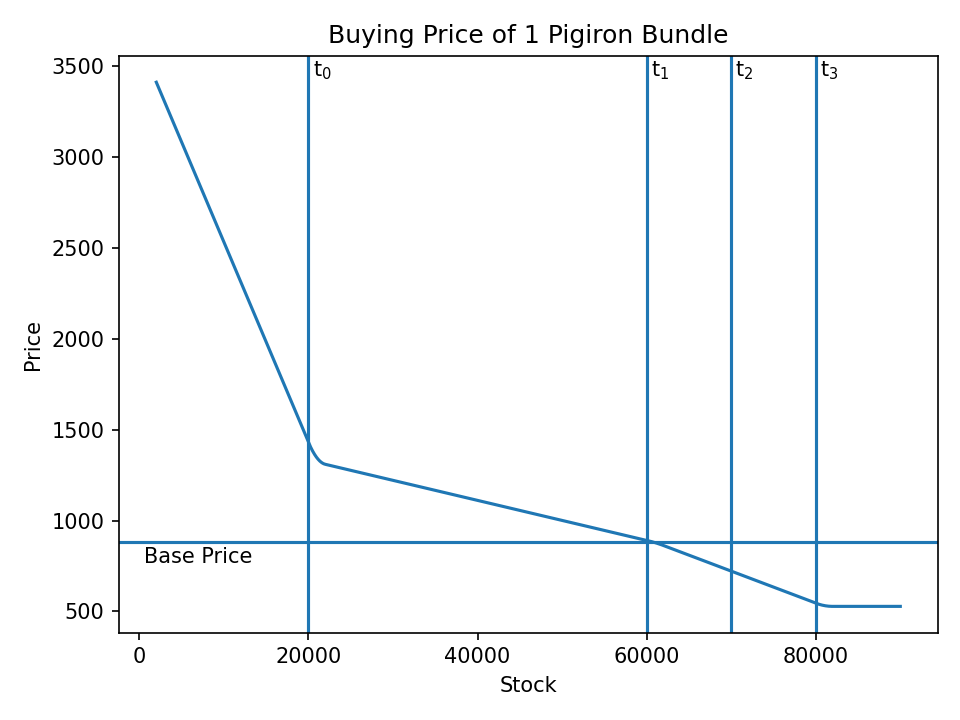
Let's assume we buy pig iron from a town with the following thresholds:
| Threshold | Value |
|---|---|
| t0 | 20000 |
| t1 | 60000 |
| t2 | 70000 |
| t3 | 80000 |
If we buy one bundle (2000), the resulting prices at different stock levels would be:
Auto Trader Discount
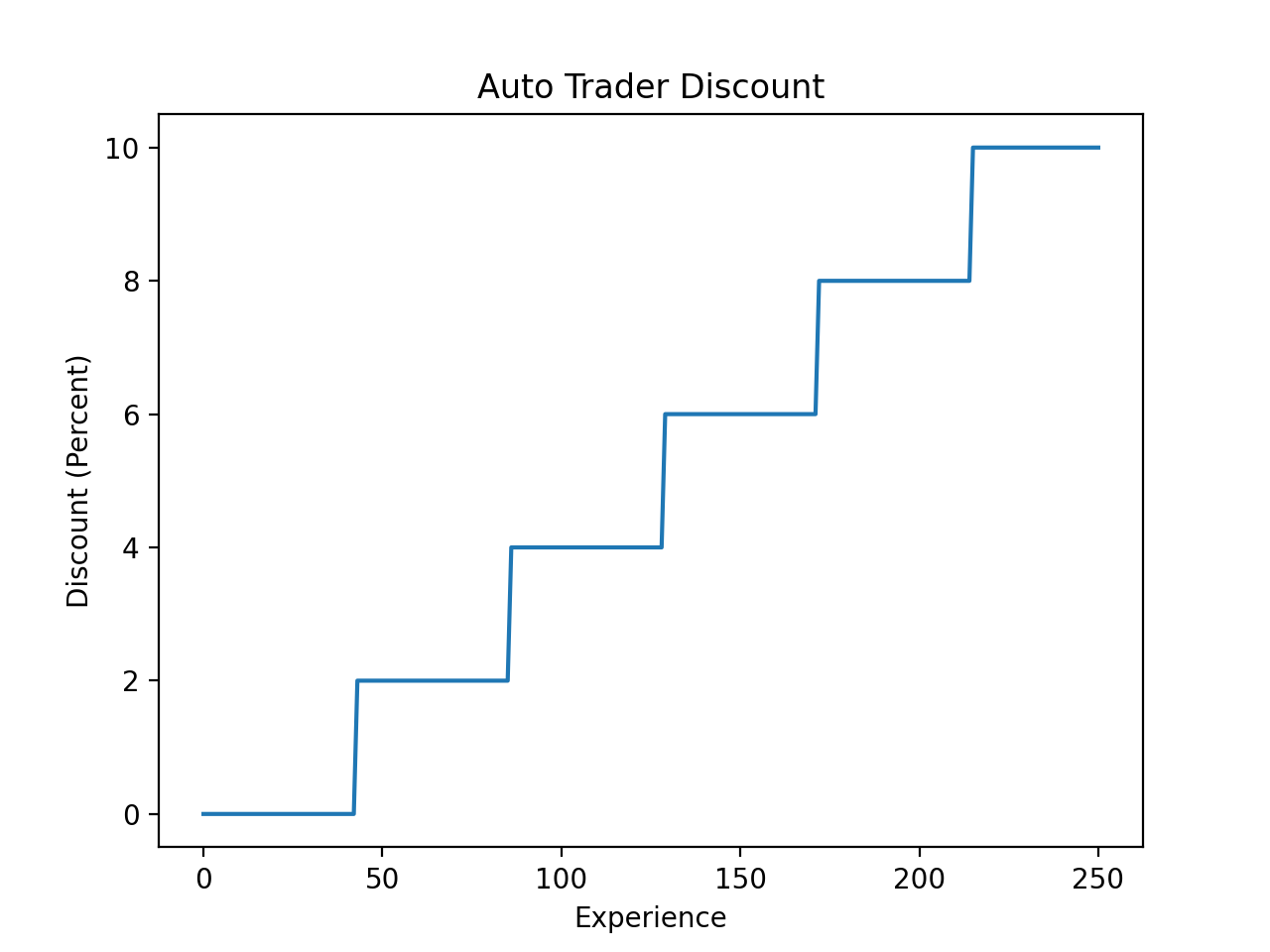
Auto traders (captains and administrators) get a discount depending on their trade skill. The discount is calculated as follows:
100 - (2 * (50 - xp // 43))
The calculation can be observed at 0x004D5347 for captains and at 0x004FF7E8 for administrators.
Since a new discount is unlocked every 43 experience, auto traders reach the maximum discount at 215 experience, way before they reach level 5 at 250 experience.
The discount is applied after the transaction's amount has been determined.