Projectiles
Ship Artillery Projectiles
The sea_battle_local_map_ship_fire_volley function at 0x0061E8EF loops over the artillery slots of the selected side.
It restricts the target coordinates to be in the cone of fire, and calls sea_battle_local_map_ship_fire_shot at 0x006214CB for every artillery piece.
The code for all plots can be found in the source code of this book.
Raw Damage
The raw damage of all projectiles of a volley is controlled through 3 tables in the sea_battle_local_map_ship_fire_volley function: Damage Component 1 at 0x00672CC0, Damage Component 2 at 0x00672CD0, and Damage Reduction at 0x00672CE4.
The vanilla values are shown in the following table:
| Artillery Type | Damage 1 | Damage 2 | Damage Reduction |
|---|---|---|---|
| Small Catapult | 32 | 60 | 480 |
| Small Ballista | 32 | 80 | 160 |
| Large Catapult | 77 | 60 | 480 |
| Large Ballista | 77 | 80 | 160 |
| Bombard | 96 | 90 | 120 |
| Cannon | 58 | 90 | 120 |
The formula of the raw damage is as follows:
def calc_raw_damage(distance: int, artillery_type: int):
return max(0, distance \
* damage1[artillery_type] \
* damage2[artillery_type] \
// (-6 * reduction[artillery_type]) \
+ \
damage1[artillery_type] \
* damage2[artillery_type])
The following image shows the plot of raw damage and distance, with the damage values of double slot weapons adjusted by 0.5.
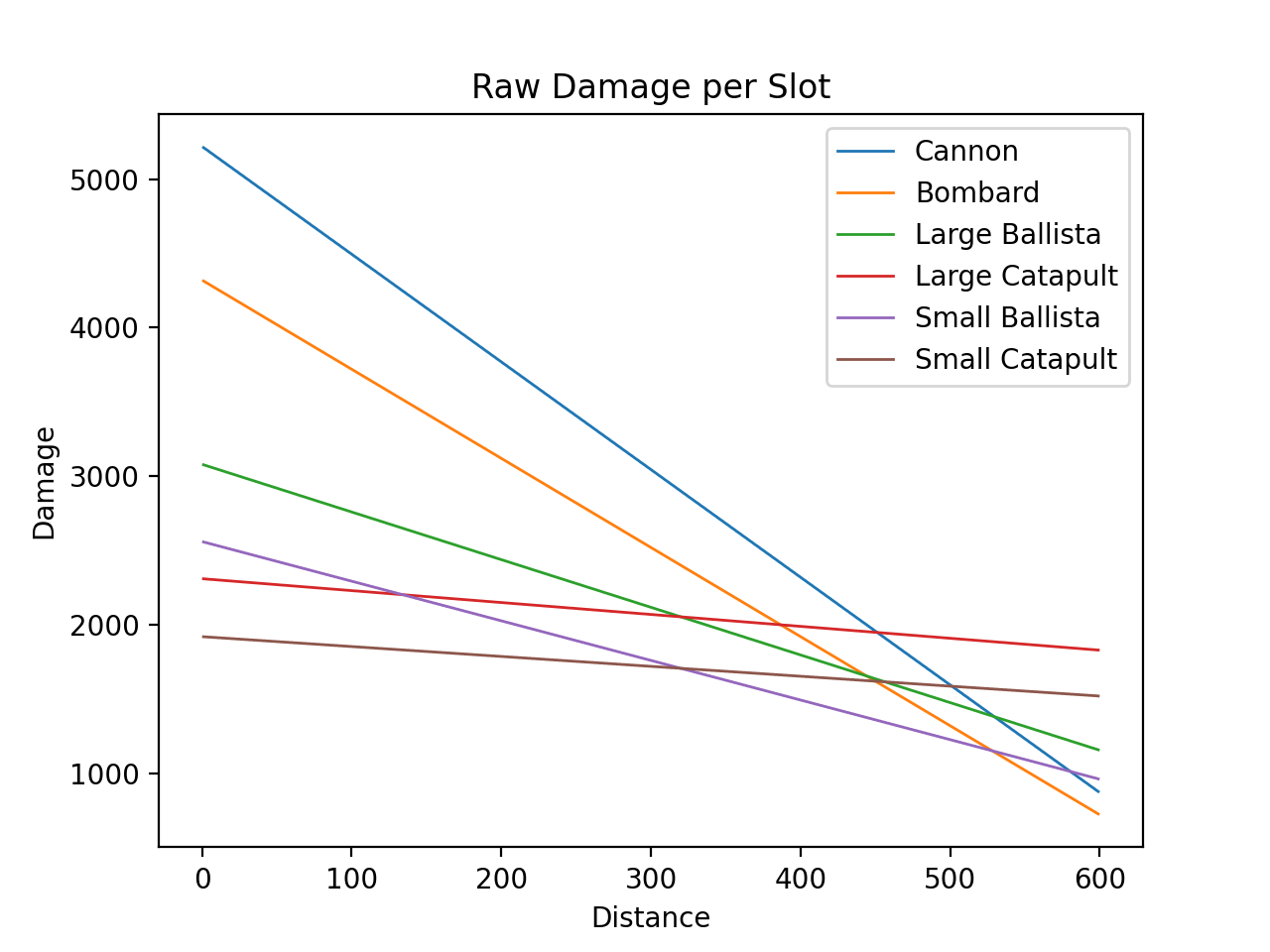
While every individual projectile is subject to minor source and destination adjustments, the distance raw damage calculation is done once for the entire volley.
Scaling
The raw damage is scaled linearly in the sea_battle_local_map_ship_fire_shot function at 0x006214CB:
def calc_scaled_damage(raw_damage: int):
return 2800 * (raw_damage // 64) // 100
The precision loss caused by the division by 64 has a slight effect on the granularity:
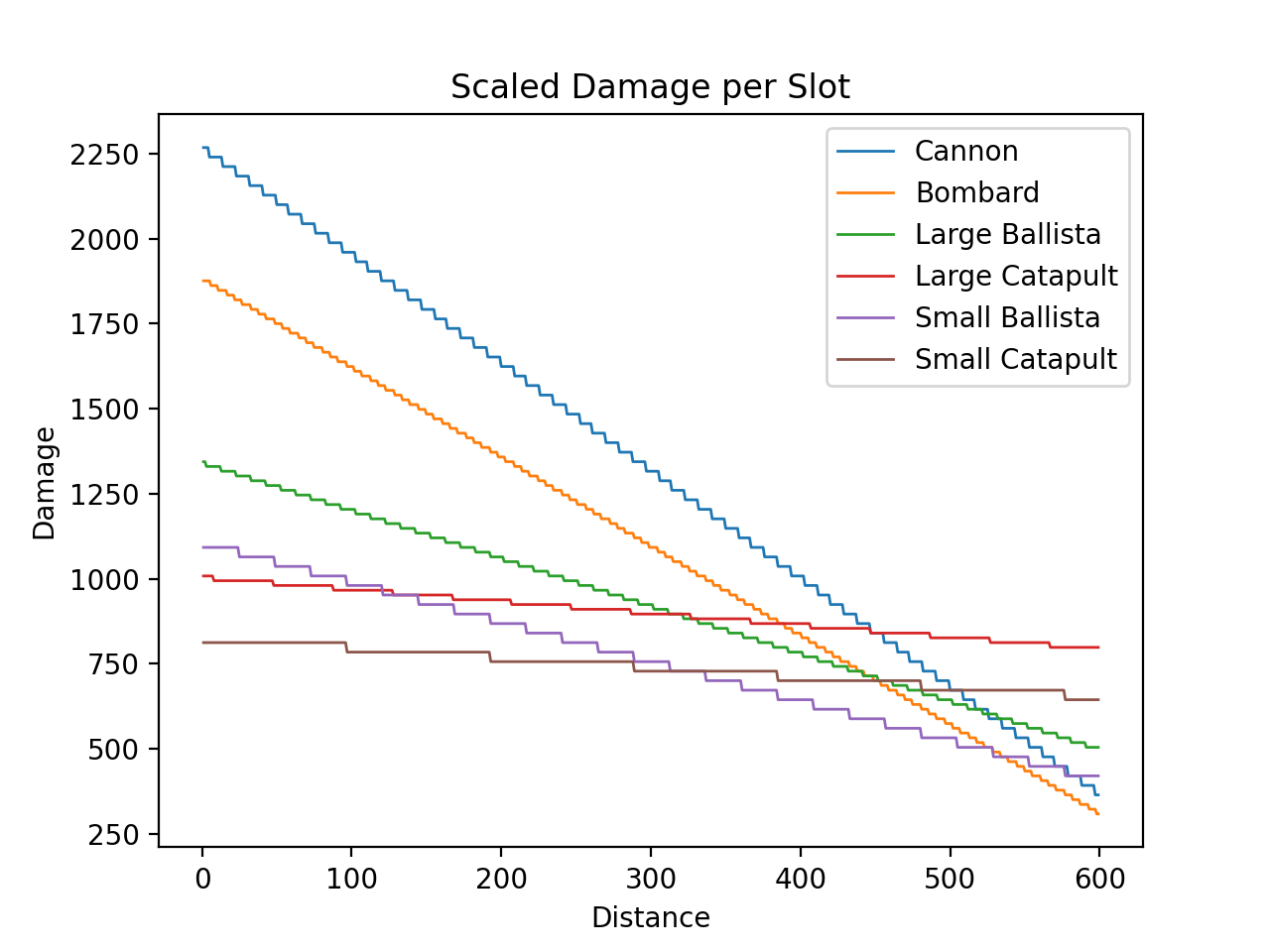
While the function is called for every individual projectile, this calculation will yield the same values for every projectile of a volley.
Captain
Then the function uses the captain's combat experience (a value between 0 for a combat level 0 and 250 for a combat level 5 captain) to increase the damage:
def apply_captain_factor(scaled_damage: int, combat_experience: int):
if not combat_experience:
return scaled_damage
else:
return scaled_damage * (6 * combat_experience // 17 + 100) // 100
This factor is roughly (ignoring precision loss through divisions) equivalent to \(\frac{3 * combat\_experience}{850} + 1\) or \(0.17647058823 * combat\_level + 1\).
The following figure highlights the impact of a captain on a projectile's damage:
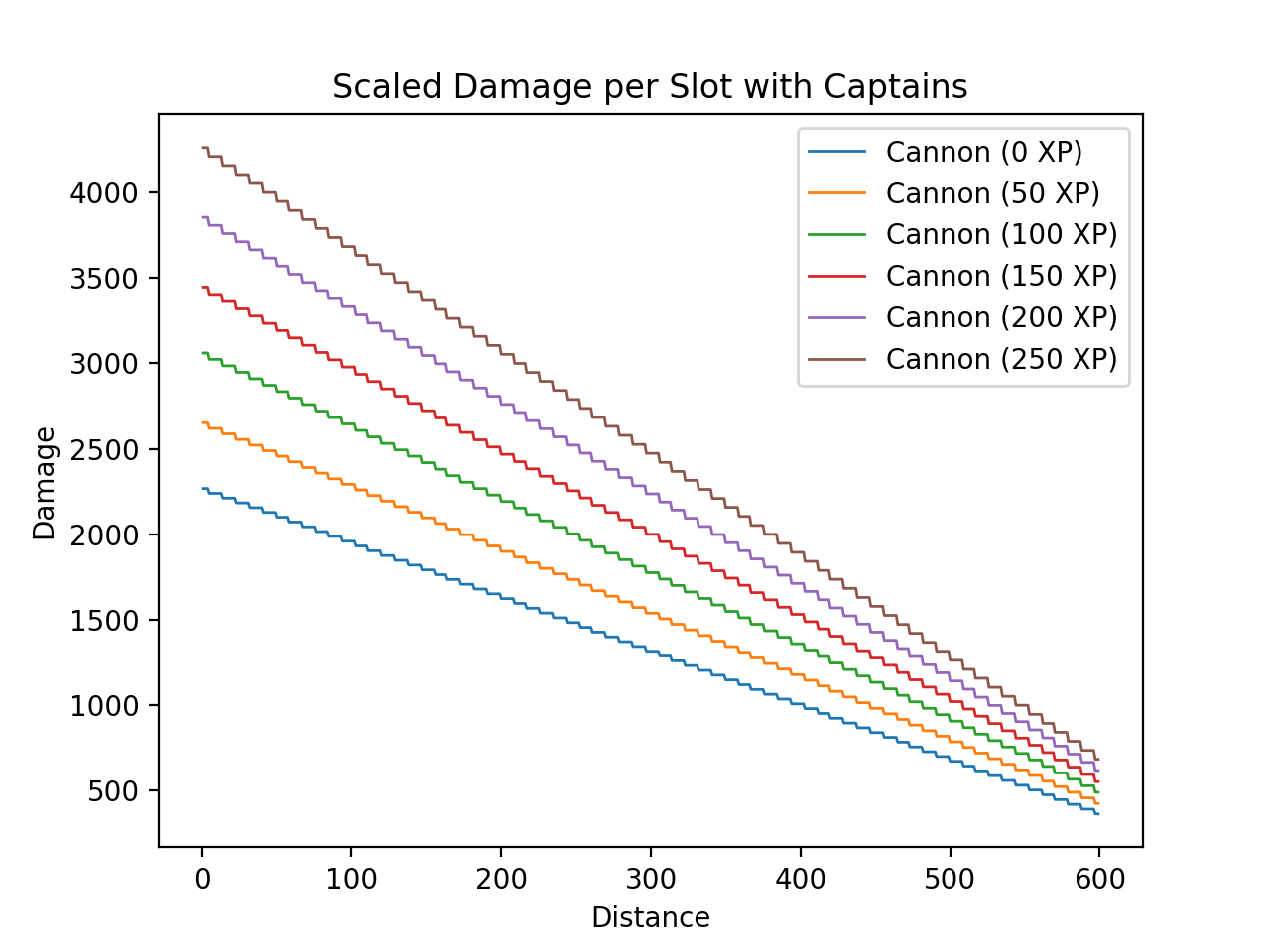
While the function is called for every individual projectile, this calculation will yield the same values for every projectile of a volley.
Difficulty and Maintenance
Then the function considers sea battle difficulty setting and the ship's current maintenance value to affect the damage as follows:
def apply_difficulty_and_maintenance(
damage: int, difficulty: int, ship_maintenance: int, is_ai: bool
):
f = min(4, max(ship_maintenance >> 8, 0))
if not is_ai:
match difficulty:
case 0: # Easy
f += 2
case 2: # Hard
f -= 2
if f > 0:
return damage + damage * (f - 2) // 20
else:
return damage + damage * (f - 1) // 20
Since f cannot exceed 6, the bonus damage from difficulty and maintenance will not exceed \(\frac{1}{5} * damage \).
While the function is called for every individual projectile, this calculation will yield the same values for every projectile of a volley.
Normal Distribution and Minimum
Then the function applies a factor with a discrete uniform (assuming the sea battle's PRNG works as intended) distribution in the discrete (up to the second decimal point) interval from 0.85 to 1.15, and enforces a minimum damage of 1:
# Discrete distribution
damage = damage * (battle_rand() % 31 + 85) // 100
# Minimum
damage = max(damage, 1)
Final Scaling
Finally the init_sea_battle_projectile function at 0x00602A90 multiplies the damage by 1.5, and stores the final damage in the projectile.